Traders
Wanted
Trade for Modern Prop Trading Firm
FTMO developed a unique 2-step Evaluation Process for traders. This Evaluation Process consists of an FTMO Challenge and a Verification and is specifically tailored to discover trading talents.
Upon successful completion of the Evaluation Process, you are offered to trade on an FTMO Account with a balance of up to $200,000. Your journey to get there might be challenging, but our educational applications, Account Analysis and Performance Coaches are here to help you on the endeavour to financial independence.
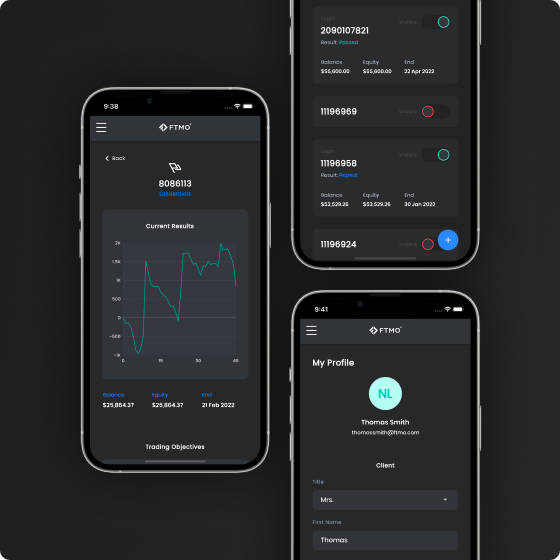
Evaluation Process
Know your Trading Objectives
Before we allow you to trade with us, we need to be sure that you can manage risk. For this reason, we developed Trading Objectives. By meeting the Trading Objectives, you prove that you are a disciplined and experienced trader.
Key Highlights
Swing Account
Pick the FTMO Account that perfectly suits your trading style and needs. FTMO Account Swing has no restrictions on holding positions over the weekend or trading during macroeconomic releases.
Scaling Plan
We aim for long-term business relationships. If you manage to be consistent and profitable, we will increase the balance of your FTMO Account by 25% every 4 months according to the Scaling Plan.
Free Trial
If you are still not sure, you have the option to try the process completely for free. The Free Trial account is a shortened version of our FTMO Challenge with the same trading conditions.
Join the team
of our successful traders
If you are ready, accept our FTMO Challenge and become our FTMO Trader.
You can even try the entire process completely free of charge.
Payout System
The default payout ratio for all FTMO Traders is set to 80%, however, an 80% share is not where we draw the line.
All FTMO Traders can request payout on-demand. The payout can be processed just after 14 days, but you also have the ability to choose your own Profit Split Day, which can be even changed up to three times. In conclusion, we make sure that you will always receive your withdrawal on your most convenient day.
If you meet the conditions of our Scaling Plan, not only do we increase the balance of your FTMO Account by 25%, the payout ratio will also automatically change to a staggering 90 %!
The most popular retail trading platforms
We offer all our clients the best trading solution in the form of our MT4, MT5, DXtrade and cTrader accounts powered by data feed directly from our pool of prime liquidity providers. We do our best to simulate the real market conditions with super-raw spreads, very low commission and no markup to all demo trading accounts with virtual funds.



Trading Instruments
We are more than just a Modern Prop Trading Firm
Find out how you can benefit with FTMO.
FTMO is one of the most reliable firms in modern prop trading industry. Here’s why.
Feedback from our traders